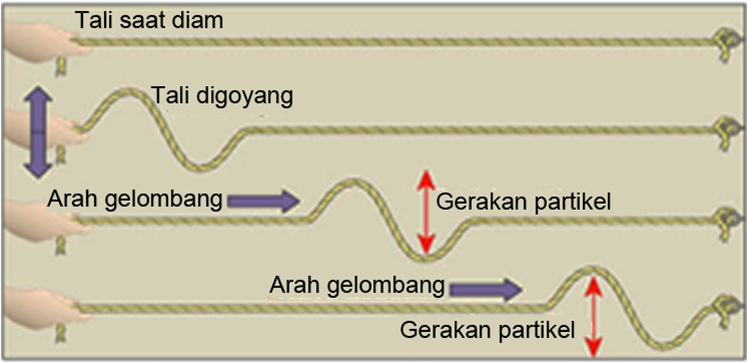
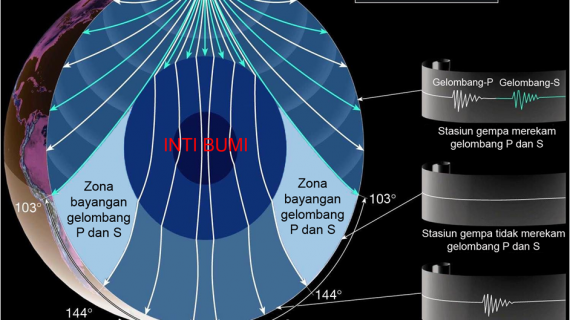
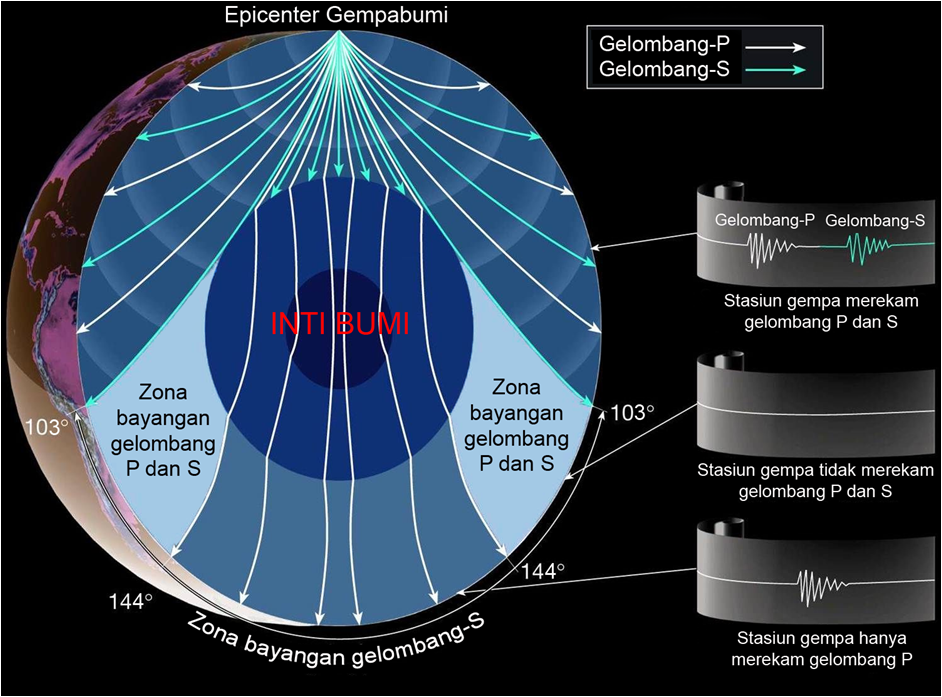
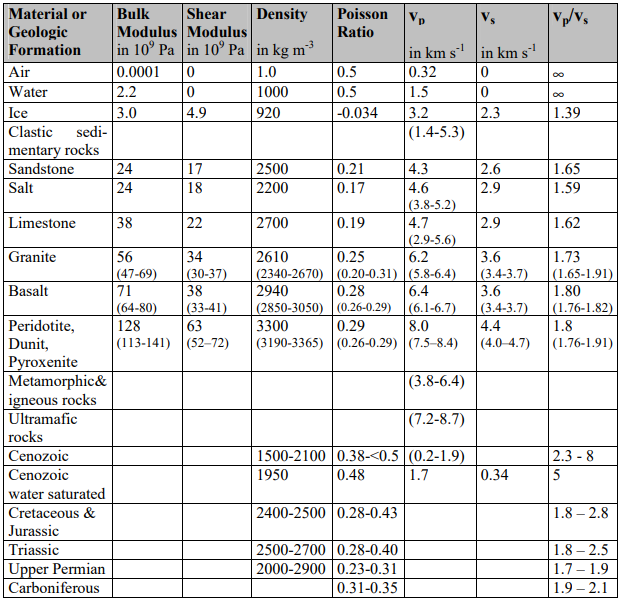
Idealisasi respon struktur terhadap beban gempa berupa kurva kapasitas struktur, yaitu kurva hubungan gaya dan perpindahan (displacement) selama respon struktur. Dalam idealisasi respon struktur ada 2 (dua) pendekatan yang digunakan, yaitu:
- Pendekatan berbasis perpindahan (equal displacement principle)
- Pendekatan berbasis gaya (equal force principle)
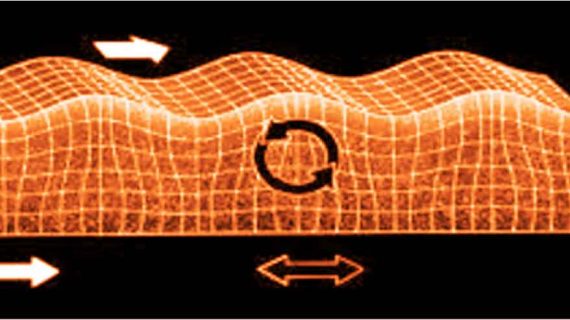
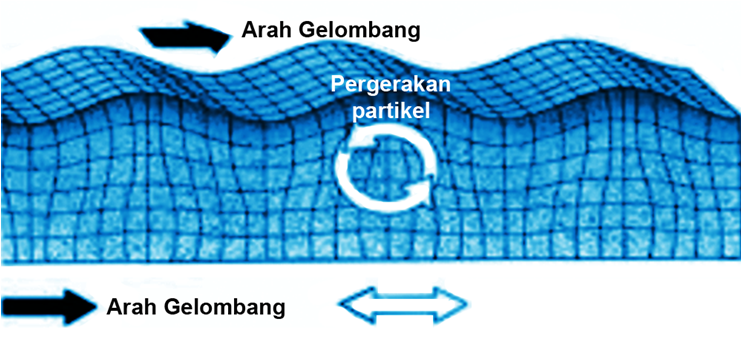
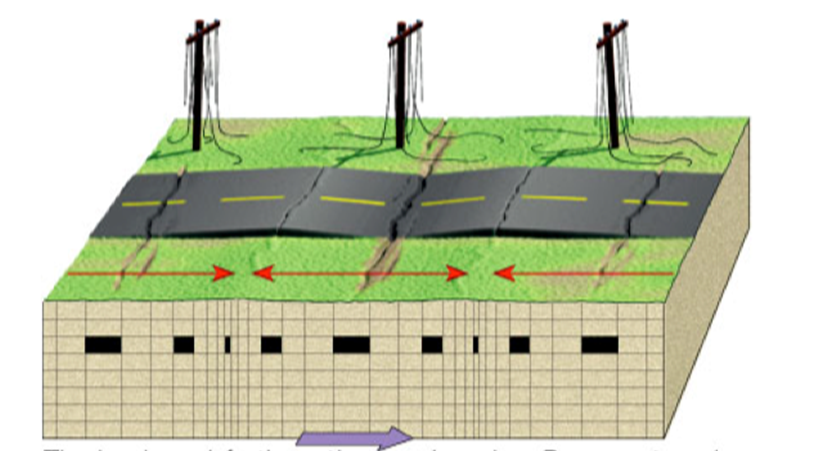
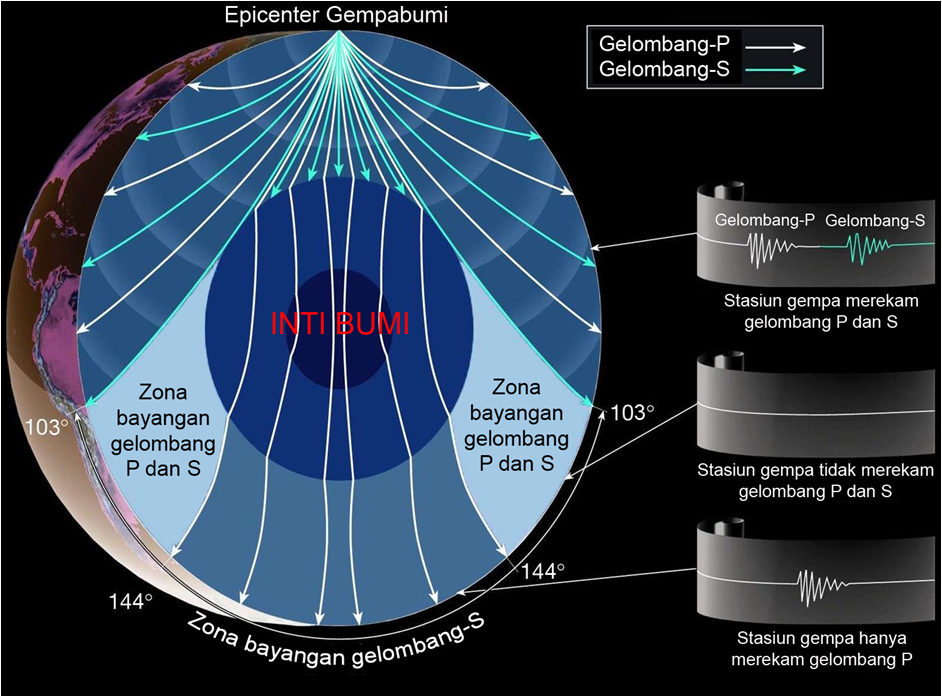
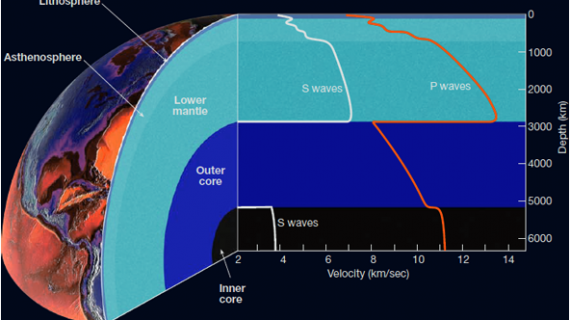
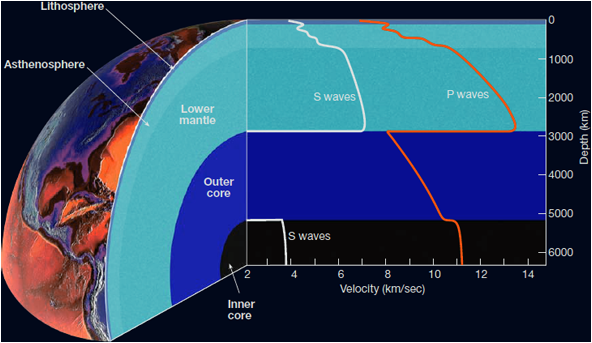
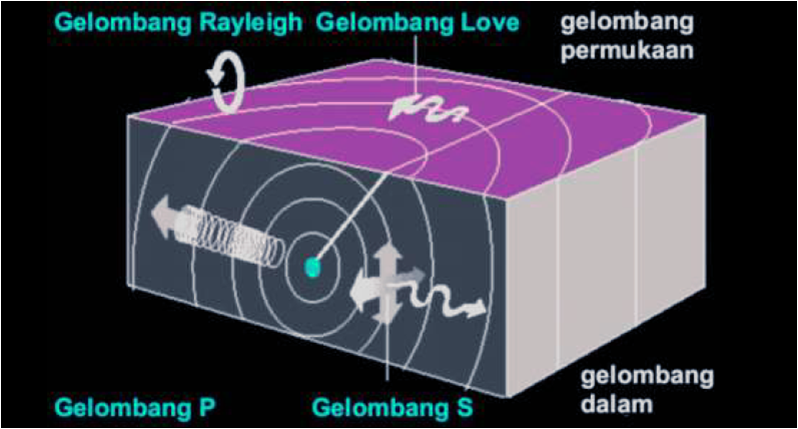
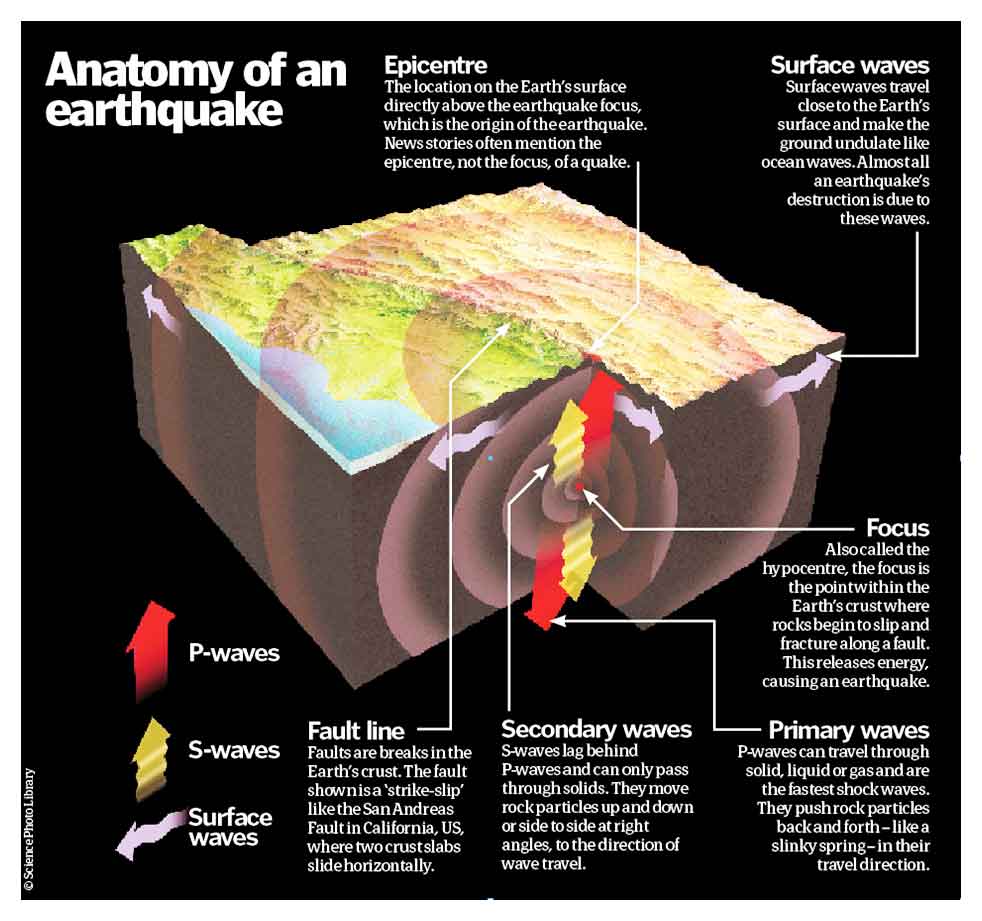
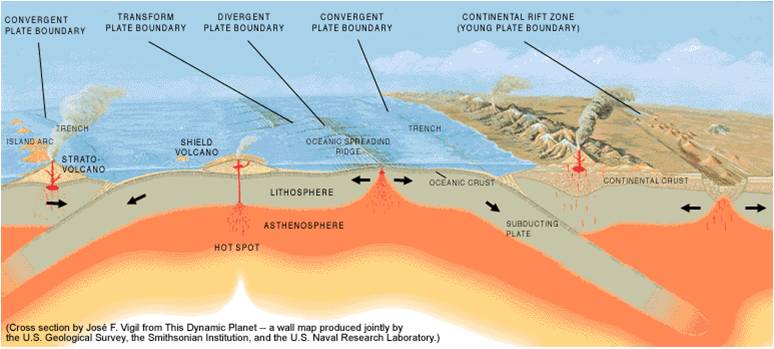
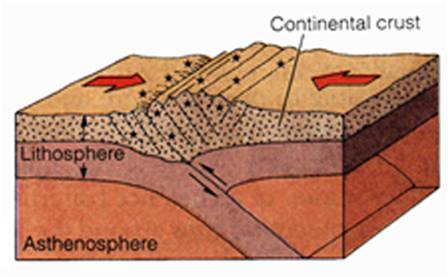
Respon Struktur Terhadap Gempa

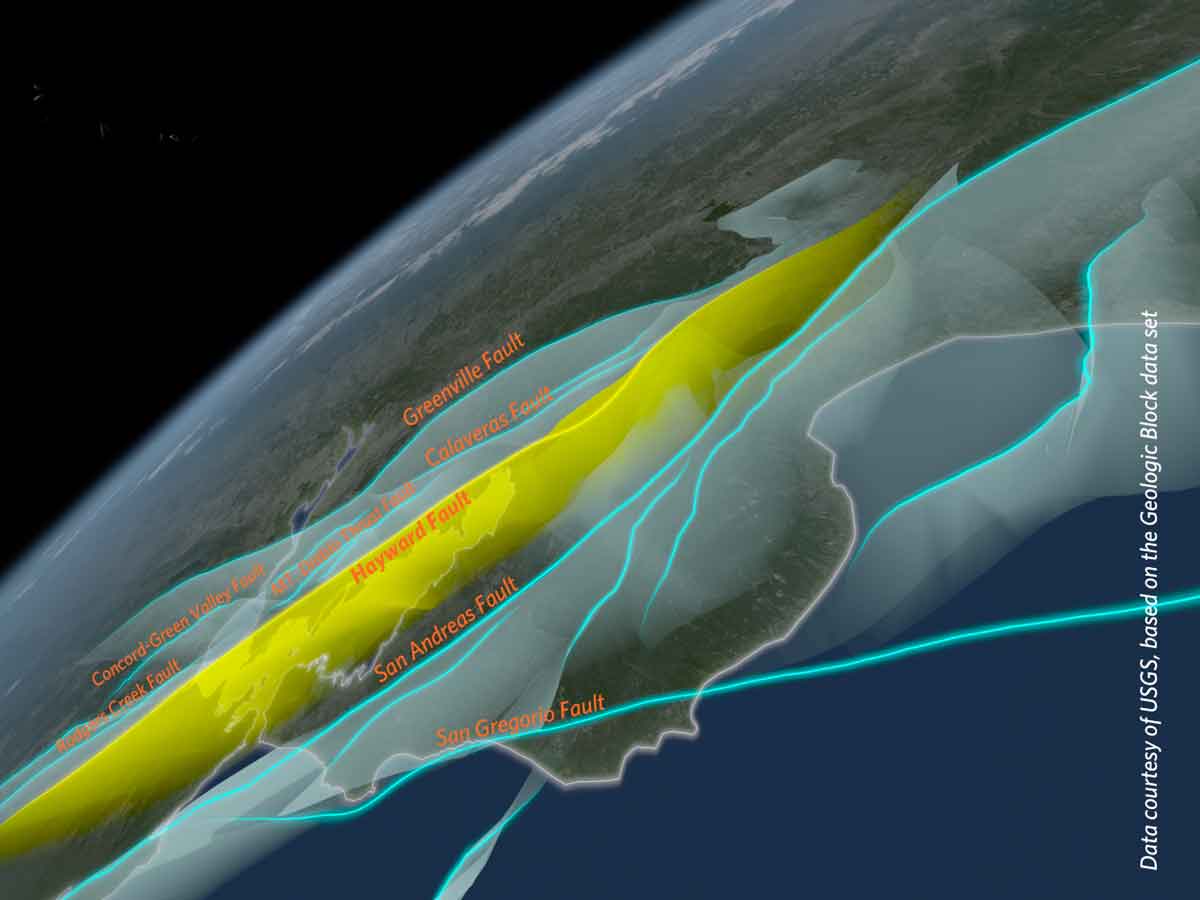
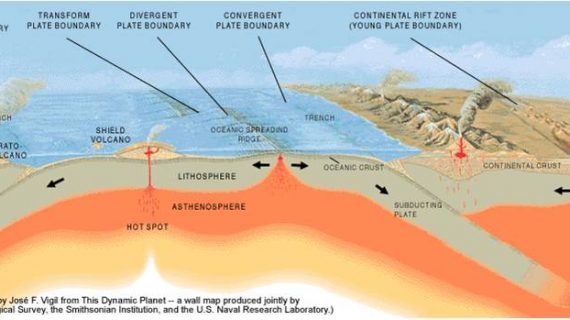
Pict source: elnuevodiario(.)com(.)ni/internacionales/69226-chile-menos-708-muertos-sismo/
Mengapa idealisasi kurva kapasitas kritis untuk desain: Kurva kapasitas menggambarkan perilaku struktur dari elastis hingga inelastis saat gempa. Tanpa idealisasi yang akurat, estimasi kapasitas dan daktilitas struktur tidak dapat dipercaya. Risiko: desain berbasis asumsi perilaku yang salah menyebabkan struktur underestimate (kurang aman) atau overestimate (tidak ekonomis). Pada contoh Gedung Alto Rio di Chile 2010, kolaps terjadi karena perilaku inelastis struktur tidak dikontrol dengan baik—kurva kapasitas yang diidealisasi tidak sesuai dengan perilaku aktual saat gempa besar.
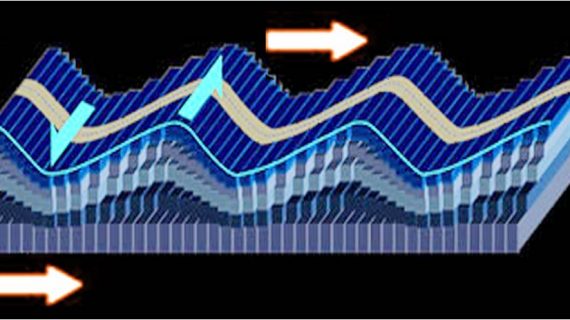
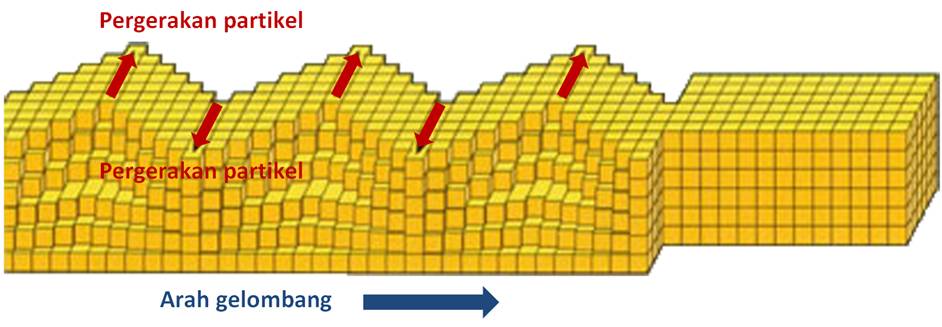
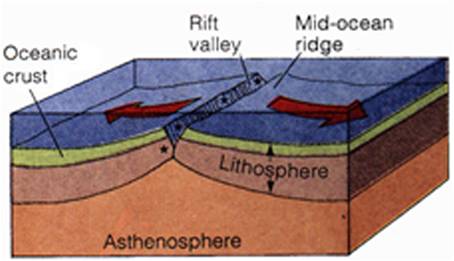
Dalam pendekatan pendekatan berbasis perpindahan jika struktur mempunyai periode panjang, maka displacement ductility yang terjadi pada sistem inelastic akan bernilai sama dengan R, atau = R, dimana R factor reduksi gaya. Seperti pada gambar berikut:
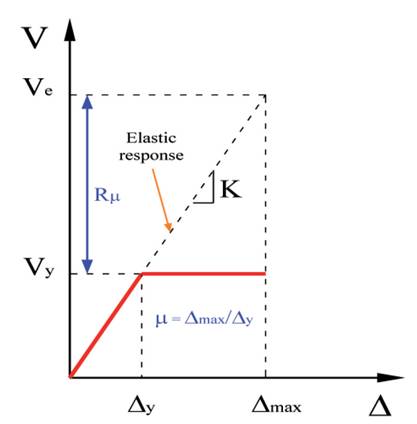
Gambar idealisasi struktur pendekatan perpindahan (equal displacement approximation)
Implikasi untuk struktur periode panjang: Asumsi μ = R berlaku untuk struktur dengan periode alami panjang (T > periode puncak respons spektral). Keputusan desain: jika struktur Anda adalah gedung tinggi, jembatan cable-stayed, atau struktur fleksibel lainnya, perpindahan inelastis yang diperlukan dapat diestimasi langsung dari faktor reduksi gaya R. Ini menyederhanakan analisis dan memungkinkan estimasi kapasitas yang lebih akurat tanpa iterasi kompleks. Namun, jika periode dominan tidak jelas, verifikasi dengan analisis respons spektral diperlukan untuk menghindari kesalahan estimasi daktilitas.
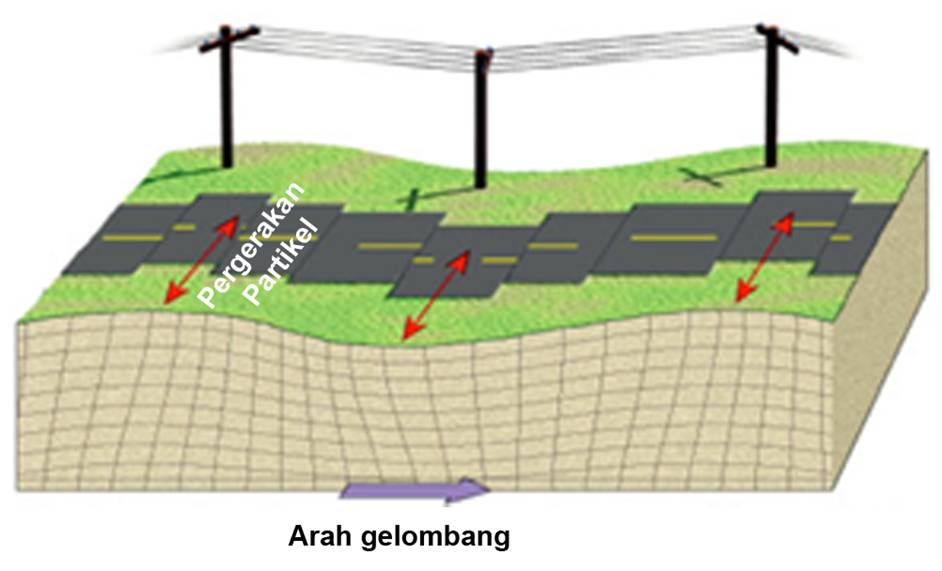
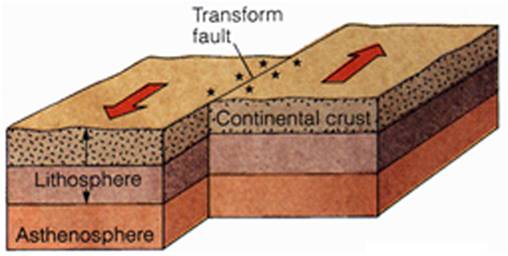
Jika struktur mempunyai periode pendek, terutama yang periode alaminya sama atau lebih pendek daripada periode respon spekral puncak, maka displacement ductility yang terjadi pada sistem inelastic akan lebih besar dari nilai factor reduksi gaya, R. Seperti ditunjukkan pada gambar berikut:
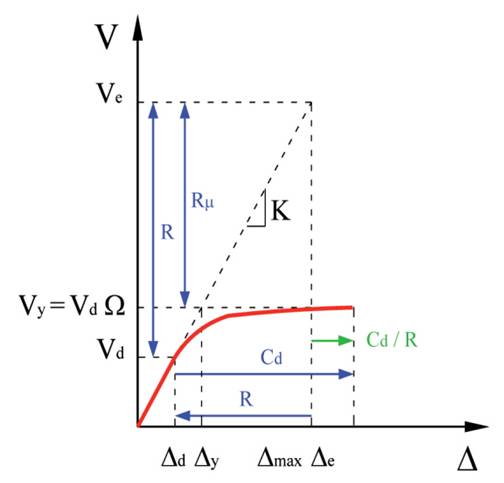
Gambar idealisasi struktur pendekatan gaya (equal force approximation)
Risiko desain untuk struktur periode pendek: Struktur dengan periode pendek mengalami daktilitas yang LEBIH BESAR daripada faktor reduksi gaya R. Ini berarti struktur harus mampu deformasi lebih jauh dari yang diprediksi R saja. Konsekuensi jika tidak dikontrol: struktur mungkin mengalami kerusakan lebih parah dari yang direncanakan, atau kapasitas penampang tidak cukup untuk menahan deformasi inelastis yang sebenarnya. Praktik lapangan menunjukkan banyak struktur pendek (gedung beton tahan gempa di area padat) mengalami kerusakan berlebihan saat gempa moderit karena daktilitas aktual tidak terprediksi dengan baik.
Sehingga hubungan antara R pada tingkat daktilitas dibedakan atas 3 (tiga) kondisi menurut periode efektif struktur sebagai berikut:
Struktur dengan periode pendek: R =(2-1)^0.5
Struktur dengan periode panjang: R =
Struktur dengan periode 0: R =1
Penerjemahan tiga kondisi periode untuk keputusan desain: Formula R di atas menunjukkan hubungan non-linier antara periode struktur dan kapasitas daktilitas yang diperlukan. Implikasi praktis: (1) untuk periode pendek, daktilitas meningkat secara non-linier (μ > R), memerlukan kontrol penampang lebih ketat; (2) untuk periode panjang, asumsi μ ≈ R menyederhanakan desain; (3) untuk periode nol (kaku), tidak ada amplifikasi perpindahan (μ = 1). Keputusan kritis saat awal desain: apakah periode efektif struktur Anda dekat dengan periode puncak respons spektral gempa lokal? Jika ya, validasi daktilitas dengan analisis non-linier iteratif diperlukan untuk memastikan kapasitas realistis
Untuk factor reduksi gaya, R, seperti yang tercantum dalam standar yang ada merupakan perkalian faktor reduksi gaya pada tingkat daktilitas dikalikan faktor kuat lebih sistem. R = R x
Sedangkan nilai faktor pembesaran defleksi, Cd, ditentukan dengan perkalian displacement ductility dengan faktor kuat lebih sistem:

Catatan lapangan tentang faktor R dan Cd: Di praktik, faktor R dan Cd yang tercantum dalam SNI 1726 adalah nilai standar yang dikalibrasi untuk sistem struktur umum. Namun, untuk struktur dengan sistem penahan gempa non-standar (hybrid, friction damper, tuned mass damper), nilai R dan Cd mungkin perlu divalidasi atau disesuaikan melalui studi khusus. Risiko: penggunaan R dan Cd standar tanpa verifikasi pada sistem non-standar dapat menghasilkan estimasi kapasitas yang signifikan berbeda dari perilaku aktual. Pada proyek-proyek inovatif, konsultasi dengan spesialis dinamika struktur disarankan sebelum penetapan final R dan Cd.
REFERENSI
[1] Julián, C., Barrios, H., Astrid, R.F., Analysis of the Earthquake-Resistant Design Approach for Buildings in Mexico, Ingeniería Investigación y Tecnología, volumen XV (número 1), enero-marzo 2014: 151-162
[2] SNI 1726:2012, 2012, Tata Cara Perencanaan Ketahanan Gempa untuk Struktur Bangunan Gedung dan Non Gedung, Badan Standarisasi Nasional, Jakarta.
Penulis: Dr. Ir Heri Khoeri, MT
Artikel ini merupakan bagian ke empat dari 5 tulisan berkaitan konsep desain struktur tahan gempa. Berikut urutan tulisan selengkapnya :
- Perkembangan Konsep Desain Struktur Tahan Gempa
- Disain Struktur Tahan Gempa Berbasis Kinerja (Performance Based Seismic Design)
- Konsep Disain Struktur Tahan Gempa Berbasis Perpindahan (Direct Displacement Based Design)
- Respon Struktur Terhadap Gempa
- Idealisasi Respon Struktur Terhadap Gempa Menurut Sni-1726-2012
Konsultasi Analisis Respon dan Idealisasi Kapasitas Struktur Tahan Gempa
Idealisasi kurva kapasitas dan parameter daktilitas (μ, R, Cd) adalah fondasi untuk estimasi akurat kapasitas struktur terhadap gempa. Kesalahan dalam idealisasi menyebabkan desain yang tidak realistis—baik underdisign (risiko keamanan) maupun overdisign (inefisiensi biaya).
Tim struktur kami melakukan analisis respon struktur yang komprehensif, termasuk: verifikasi periode efektif terhadap spektral respons lokal, validasi kurva kapasitas dengan perilaku non-linier iteratif, dan penentuan faktor daktilitas dan reduksi gaya yang realistis untuk sistem penahan gempa spesifik Anda. Untuk struktur non-standar atau sistem inovatif, kami melakukan studi khusus untuk memastikan parameter desain konsisten dengan standar dan perilaku aktual.
PT Hesa Laras Cemerlang
Komplek Rukan Mutiara Faza RB 1
Jl. Condet Raya No. 27, Pasar Rebo, Jakarta Timur, Indonesia
- ✉️ Email: kontak@hesa.co.id
- ☎️ Telepon: (021) 8404531
- 📱 Hotline: 081291442210 / 08118889409